To make the concept of gear ratio easier to understand, let’s first review some properties of circles. The radius of a circle is defined as the length from the center of the circle to the outside of the circle. If we draw a line that starts at one side of the circle, goes through the center, and then stops at the opposite side of the circle, we would have the diameter of the circle. The diameter is twice as long as the radius. Finally, if we measured the distance around the circle, we’d get the circumference. It turns out that the circumference is equal to the diameter multiplied by Pi. Pi is often represented by the Greek symbol, , and is equal to 3.1415927… or a very strange ratio of 22 / 7 !

Now we can apply these concepts to look at how gears work. Look at the gears in the diagram. The radius of the gear is the distance from the center of the gear (where it rotates) to the outside of the gear. If gear A measures 10 in [25.4 cm] in radius and gear B measures 5 in [12.7 cm] in radius, then the radius of gear A is twice as large as gear B. We say that the gear ratio of gear A to gear B is 2:1. Additionally, we know that the diameter is twice the radius, and the circumference is times the diameter, so if the radius of gear A is twice the radius of gear B, then the circumference of gear A is also twice that of gear B. In the diagram of the two gears you can see that twice the circumference means that the gear has twice the number of teeth.

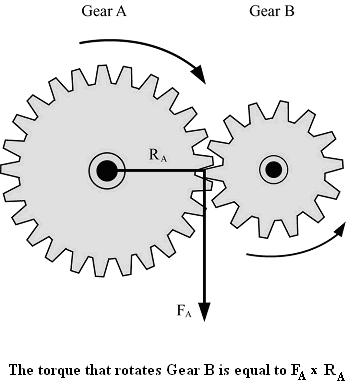
Imagine gear A starts to rotate. As its teeth touch the teeth of gear B a force is exerted. In the diagram this is shown as F_A. If gear A rotates clockwise, the teeth of gear A push downwards on the teeth of gear B. This will cause gear B to move counter-clockwise. In this case, gear A is called the driving gear, and gear B is called the driven gear. If the gear ratio of A to B is 2:1, then there are twice as many teeth on gear A as on gear B. If you look where the two gears connect, you can see that the gear teeth alternate, that is a tooth from gear A is followed by a tooth from gear B, then one from gear A, then one from gear B, and so on. Since we said that gear A has twice as many teeth as gear B, then it will take twice as long for gear A to rotate once all the way around. This means that the gear A will rotate two times slower than gear B. This is very useful because we now have a way of speeding up and slowing down torque rotation!

We said that a gear that is half the size of another will rotate twice as fast. A gear that is one fourth the size of another will rotate four times as fast. This relationship is called a reciprocal. ½ is the reciprocal of 2, and ¼ is the reciprocal of 4. To find the reciprocal of a number, you take one divided by the number.

Reciprocal of number = 1 ÷ number

We say that the gear ratio of two gears is the reciprocal of the ratio of their rotation speeds.

To calculate torque on two gears, use the formula for torque.

Torque = Force · Length of lever arm

Gear A is exerting a force on gear B, but remember Newton’s third law states gear B will, in turn, exert an equal force back on gear A. This means that the force on each gear is the same. The force applied to each gear occurs where the gear teeth are in contact on the outside of each gear, so the length of the lever arm for each gear is equal to the radius of the gear. Since the radius of gear A is twice the radius of gear B, the torque on gear A will be twice the torque on gear B. This is very useful because we now have a way of enlarging or reducing torque!

Let’s review what gear ratio means. If the gear ratio of gear A to gear B is 4:1, we know the following. The radius, diameter, and circumference of gear A are all four times larger than gear B. We know that the torque on gear A will be four times greater than the torque on gear B. Finally we know that gear A will rotate at one fourth the speed of gear B. A larger gear will rotate slower than a smaller gear and have a greater torque, and the two gears will rotate in opposite directions.

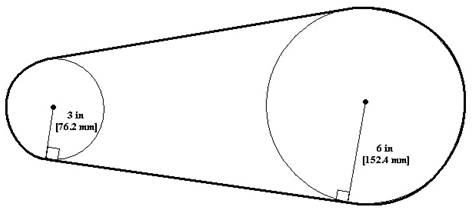
When working with pulleys connected by a belt, the principles behind gear ratio, rotation speed, and torque are exactly the same. In the diagram, the pulley on the left has a radius equal to half the radius of the pulley on the right. This means that the pulley on the left will rotate twice as fast, but will have only half the torque.

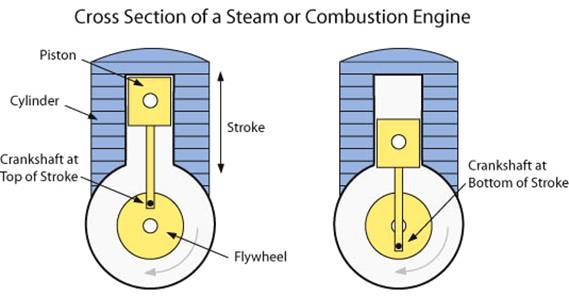
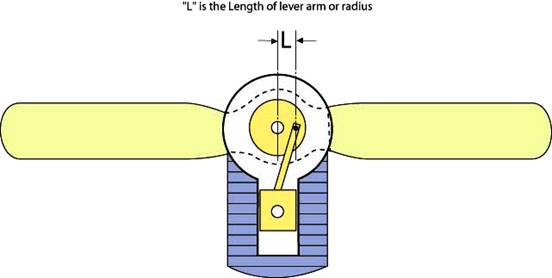
Torque and gear ratios are important in designing what is called the hovercraft’s transmission. Lightweight engines produce most of their horsepower at high rpm (revolutions per minute). Unfortunately, this would spin a propeller too fast for safety. To get maximum thrust from a propeller, the tips of the blades should rotate between 683.4 and 714.5 mph [1100 – 1150 km/h]. At speeds above this, the flow of air begins to detach itself from the propeller, decreasing efficiency and increasing noise. Propeller tip speed on a hovercraft should never run higher than 460 mph [641 km/h] tip speed for safety. It's often necessary to use a belt or gear driven system to slow the propeller but still let the engine reach its maximum horsepower. Using a small pulley on the engine and a larger pulley on the propeller will allow the propeller to turn more slowly than the engine. This is ideal for a two or four-bladed propeller, since they produce more thrust at slower speeds. They also produce less noise and develop more thrust per horsepower than fans with many blades.

Recall that the pitch of a propeller refers to the angle at which it is set, and a greater pitch means that the propeller can push more air and produce more thrust. Pushing greater amounts of air, however, requires more torque. If the pitch of the propeller is too great, it will strain the engine, making it unable to reach its maximum rpm. Too great a pitch can also cause the blade to "stall" where upon it will push almost no air. Choosing the right propeller pitch to maximize thrust while still allowing the engine to reach its maximum rpm is a very important step in designing a hovercraft.

The graph below is an example of what the characteristics of an engine and propeller could look like. The red curve shows the power output of the engine. Notice how it increases as rpm increases until it reaches a maximum at about 3400 rpm. It then quickly decreases as the speed continues to increase. The green curve represents how much power needs to be supplied to the propeller in order to keep it turning at the given speed. Notice how the faster the propeller spins, the more power is required. At lower rpm’s the red curve is higher than the green curve, meaning that the engine produces more power than is needed to keep the propeller spinning. At about 3700 rpm, the two curves intersect, meaning that the engine produces just enough power to keep the propeller spinning at that rpm. This is the most efficient engine speed to run at because no engine power is being wasted. Notice that at higher rpm’s the engine cannot produce the horsepower necessary to power the propeller.

This is only an example power profile. In fact, this graph could change drastically depending on the conditions the hovercraft is operating in. For example, the propeller’s curve can change quite a bit depending on if wind is blowing, and on what direction it’s blowing. No matter how the propeller or engine power profile changes, the engine speed at which the two curves intersect will indicate the point of maximum efficiency and maximum static thrust.

Continue to Experiment 10.1