When a hovercraft turns, it continues to travel in the same direction for a while before it finally changes direction. This is due to its momentum. Momentum is defined as the mass of an object multiplied by its velocity.

Momentum = Mass · Velocity

Newton’s first law states that an object in motion tends to stay in motion. The momentum of an object is a sort of way to describe just how much the object tries to stay in motion. Let’s say there are three objects coming toward you, and you have to try to stop them. The first is an empty shopping cart rolling at 5 mph [8 km/h], the second is a small car traveling at 5 mph [8 km/h], and the third is an identical small car traveling at 50 mph [80 km/h]. If we calculate the momentum of each one, the shopping cart would have the least momentum because it has the lowest mass times velocity. The 5 mph car would be second, and the car going 50 mph would have the greatest momentum. We can probably imagine that the shopping cart would be easy to stop. Stopping the car going 5 mph would be much harder, but we could probably get it stopped after pushing it for a while. It’s safe to say that the car going 50 mph, however, would push you out of its way!

Newton’s first law can now be rewritten to say the following: An object’s momentum tends to stay the same. Remember that velocity is a measure of both speed and direction, so when the object’s momentum tries to stay the same, its velocity tries to stay the same. This means that the direction of travel also tries to stay the same. This explains why the hovercraft initially keeps going in the old direction when you try to turn it. Its momentum is carrying it in the old direction and wants to keep going in the old direction. Only after exerting enough thrust to push it in the new direction will the momentum finally change.

Rewrite Newton’s second law using momentum. Remember that Newton’s second law states that:

Force = Mass · Acceleration.

It was stated earlier that acceleration can be defined as a change in velocity, so we restate Newton’s second law:

Force = Mass · Change in Velocity

Since momentum is mass times velocity, let’s go one step further:

Force = Change in Momentum

Any time we want to change an object’s momentum, we have to exert a force on it. The greater the change, the more force is required.

So far we’ve rewritten Newton’s first and second laws to include momentum. If we do the same with Newton’s third law, the result is known as the Law of Conservation of Momentum. Remember that Newton’s third law states that for any action there is an equal and opposite reaction. This also means that for any force, there is an equal force acting in the opposite direction. Since we know that forces lead to changes in momentum, we can also say that changing the momentum of one object means that the momentum of a neighboring object will change by an opposite amount.

Imagine a game of billiards in which you shoot at the eight ball. Right after you shoot, the cue ball has momentum as it travels towards the eight ball, but the eight ball isn’t moving and so has no momentum. After they collide, the momentum of the eight ball is increased as it rolls away, but the momentum of the cue ball is decreased as it slows down or even stops. During the collision, the momentum of both balls change. If you add the momentum of the two balls before and after the collision, you’ll find that the total momentum doesn’t change during the collision. The eight ball’s momentum increases by the same amount that the cue ball’s momentum decreases. The momentum of the system, or everything involved in the collision, remains the same. This is what is meant by Conservation of Momentum.

Returning to the hovercraft turning, the momentum of the hovercraft is changing. The law of conservation of momentum says that the total momentum of everything involved in the system stays constant. Can you think of what else is changing its momentum in order to balance the hovercraft’s change in momentum? Remember that in a turn, the rudders change the direction of the airflow blowing out behind the hovercraft. The rudders are essentially changing the momentum of the air. When you add the change in momentum of the air to the change in momentum of the hovercraft, the total momentum again stays the same.

When turning in a vehicle, you often feel a force that pulls you towards the outside of the turn. Although this outward pull is often called centrifugal force, it’s actually not a force at all. It is the Law of Inertia at work. Remember that an object in motion tends to stay in motion. When the vehicle turns, your body wants to keep going straight. Refer to the diagram of the ball on a string that is spinning around in a circle. The inertia of the ball tries to make the ball travel in a straight line, but the string pulls on the ball, making it travel in a circle. The inward force on the ball due to the tension in the string is called centripetal force. A constant centripetal force keeps the ball traveling in a circle. If the string were to break, the ball would instantly start to travel in a straight line according to the Law of Inertia.

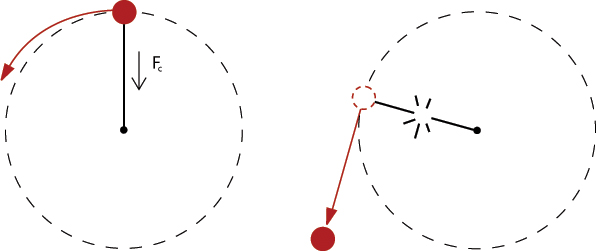
The same thing occurs when riding in a car as it goes around a curve. Instead of the tension in the string, friction between the tires and the road provides the centripetal force that pulls the car around the curve. Your body, however, wants to continue traveling in a straight line. Although it seems like your body is being pulled to the outside of the car, it is actually the car being pulled inward while you try to continue traveling straight. This is why the outward centrifugal force doesn’t really exist. Your seat belt or the wall of the car must push against you in order to accelerate you around the turn with the car.

In a hovercraft, there isn’t enough friction between the craft and the surface it’s hovering over to provide the centripetal force necessary to turn in the same way a car does. The centripetal force must instead be provided by directing the hovercraft’s thrust partially towards the inside of the curve. This is why in the pictures of the turning hovercraft, they appear to be moving sideways. The hovercraft must turn towards the inside of the curve and use its thrust to provide the centripetal force necessary to pull it around a curve. This is called vector thrust. Some of the thrust is used to keep the hovercraft moving while the remainder is used to turn the craft or to overcome the craft’s tendency to continue in a straight line.