DiscoverHover CURRICULUM GUIDE #4
MATHEMATICAL GROUNDING
© 2006 World Hovercraft Organization

The knowledge of mathematical concepts and notation is crucial to any hovercraft design, engineering, science, and testing. These are the elements that combine to express how things are and what they do. Four arithmetic operators are the foundation of the mathematical framework. Two of these arithmetic operators are addition and subtraction; their symbols are + and − respectively. The third operator is multiplication, which is represented by one of three symbols: the dot ·, the cross, ×, and the asterisk ∗. When multiplying normal numbers, these symbols are interchangeable; there are some distinctions made in certain specialized areas. Multiplication is also indicated by two quantities immediately adjacent to one another, for example, 2x represents 2 multiplied by x. The fourth arithmetic operator is division, which can also be represented by more than one symbol, either the division sign ÷ or the slash ⁄ (also called a solidus).

The Greek capital letter Delta (Δ) is used to designate a change or difference. For example, a change in mass over a period of time may be written “Δm”, and the height of an object (the difference between the altitude of the bottom and that of the top) may be written Δy.

Physical concepts such as distance, time, mass, and temperature can be completely defined by a numerical value (magnitude). These concepts are scalar quantities. Other physical concepts such as displacement and velocity are, respectively, distance and speed, but with the addition of direction. These concepts are vectors. Vectors have numerical value (magnitude) and direction, unlike scalars, which have only numerical values (magnitude). A vector is often illustrated as an arrow; the length of the arrow is the magnitude and the direction of the arrow is the direction of the vector.

Another way of looking at vectors and scalars is the number of dimensions they occupy. The world as we interact with it has three dimensions: length, depth, and height. The surface of a sheet of paper has no depth, so it only has two dimensions; a line has one dimension; and a single point has zero dimensions. A scalar quantity, since it has no direction, is a zero-dimensional quantity. A vector is a one-dimensional object, since there is one direction in which it can be measured. If you have two vectors in different directions, they are contained in what is called a plane, a two-dimensional space. The more differently-directed vectors a space can contain, the more dimensions it has. However, the principles are the same for any space with at least two dimensions, so that is the most that will be discussed in this guide.

Vector quantities require a scalar quantity for their specification (magnitude of the vector), as well as a direction. Examples of vector quantities are displacement, velocity, acceleration and force.

Remember, physical concepts that require one numerical quantity for their complete description are scalar quantities; physical concepts that require two numerical quantities for their complete description are vector quantities.

Suppose a hovercraft travels for 2 hours at a speed of 48.28 km/hr [30 mph]. Speed is completely defined by the numerical value of 48.28 with the unit km/hr. The distance traveled by the hovercraft is 96.56 km [60 miles]. The distance is completely defined by 96.56 km. Since speed and distance require only a numerical value for their complete description, speed and distance are scalar quantities.

Figure 4-1 shows a hovercraft traveling north at 48.28 km/hr (30 mph) for two hours, then traveling east at the same speed for an additional two hours. The displacements north and east are both 96.56 km (60 miles) and are indicated by arrows of proportionate length pointing in those directions. The resultant displacement, which is the sum of the actual displacements, is shown by the diagonal arrow. This calculates to be 136.6 km [85 miles] (numerical value) in a northeast direction.

Figure 4-1: A hovercraft travels north and then east
Image ©2005 DiscoverHover

Note that with vectors the location of the arrow does not affect the magnitude. Two vectors, A and B, are shown as follows:

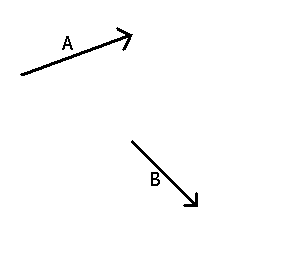
Figure 4-2: Two vectors
Image ©2005 DiscoverHover

To add the vectors in Figure 4-2, move one so that its arrow begins at the point of the other one. Since the placement of the arrow does not affect the meaning, it does not matter which one you move:

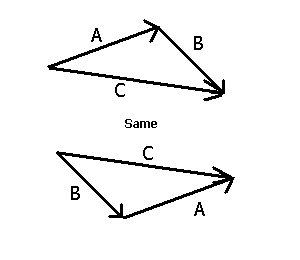
Figure 4-3: Graphical addition of vectors
Image ©2005 DiscoverHover

If a vector changes over time, the ? notation is used to indicate the change. For example, if the vector labeled A in Figure 4-3 changes over time to become the vector labeled C, then ?A would be vector B, because that is the amount by which A changes. This is illustrated most clearly in the top half of the Figure 4-3.

Unit vectors are single units in a particular direction (see Figure 4-4). It is often convenient to make these steps along the x and y axes. Any two-dimensional vector can be expressed as so many steps in the x direction followed by so many in the y direction. Thus a vector A can be written as

A = A_x (x direction) + A_y (y direction)

Or, using a common notation where a unit in the x-direction is denoted i and in the y-direction j

A = A_x i + A_y j

The coefficients A_x and A_y are known as the components of the vector in the x and y directions respectively.

Figure 4-4: Unit vectors
Image ©2005 DiscoverHover

Multiplying a vector by a scalar produces a vector in the same direction as the first vector but with the magnitudes multiplied. (See Figure 4-5.) This means that unit vectors can be multiplied by scalar quantities to determine components that can be added together to make any vector. Vectors A and B in Figure 4-5 are an example:

Figure 4-5: Two vectors in a coordinate plane
Image ©2005 DiscoverHover.

These vectors can be described as 3i + 2j and 1i - 3j respectively. To add them, first add the horizontal components to each other, then add the vertical components to each other; the result is vector 4i - 1j.

Figure 4-6: Graphical addition of vectors in a coordinate plane
Image ©2005 DiscoverHover

Figure 4-6 illustrates that vector 4i - 1j is the same as the vector that results from sliding vector A to B to add graphically as shown in Figures 4-2 and 4-3. These methods can be used with all vectors such as forces, velocities, and accelerations. It is important to remember that only like quantities may be added to each other; for example, forces may be added to forces, but forces cannot be added to velocities or to accelerations.

Quiz Questions:

1. Identify scalar and vector quantities from the following: speed; displacement; velocity; pressure; acceleration; distance; temperature; force; momentum; mass; length and time.
2. Which one of the two types of quantities, scalar or vector, contains more information?
3. Simple addition is used to add two scalar quantities; how do we add two vector quantities?