DiscoverHover CURRICULUM GUIDE #14
PRESSURE AND BOYLE'S LAW
© 2005 World Hovercraft Organization

Since hovercraft hover by using a pressurized bubble of air, it would be helpful to investigate the properties of gases and other states of matter.

Matter exists in three different phases: solid, liquid and gas. Solids and liquids possess certain common properties. They are incompressible, and their densities stay nearly constant if the temperature changes while the pressure remains constant. Gases compress easily and their density changes with temperature even if the pressure stays constant.

Looking from a different perspective, liquids and gases are commonly known as fluids. ‘Fluid’ comes from a Latin word that means “to flow”. Fluids flow to take the shape of the container they are in. Solids, on the other hand, do not have this property. In this lesson we consider the properties of fluids at rest and in motion.

Blaise Pascal
1623 – 1662

When we apply a force to a solid we observe that a stress is developed inside the solid. The ability to flow makes a fluid unable to sustain a shearing stress (a stress where particles are sliding against each other). Under static conditions only the force which is normal, or perpendicular, to the surface of the fluid need be considered. Irrespective of the shape of the fluid, the force everywhere is at a right angle to the edge of the fluid. The magnitude of the normal force per unit surface area is called the pressure. The SI unit of pressure is N/m². This unit is given the SI designation pascal (Pa): 1 N/m² = 1 pascal = 1.45×10^-4 lb/in².

Pressure does not have directional properties; therefore, it is a scalar quantity. When you swim underwater, the water exerts pressure and presses you from all directions. It should be noted that pressure is produced by a force, which is a vector quantity, but pressure itself is a scalar quantity.

Any small element of mass Δm and volume ΔV has a density ρ given by:

ρ = Δm / ΔV

If the density of a body has the same value everywhere inside the body, then the density of the body is the ratio of its entire mass to its entire volume. Density does not depend on direction, so it is a scalar property. The unit of density is kg/m³ or lb/in³.

In equilibrium, a fluid has no net force or torque acting on it. Picture a container of water. All the water in the container has the same density. Now picture a disc-shaped region in the water. The disc is at height y and has a thickness Δy. The area of a face of the disc is A. The mass of this element is Δm = ρ × ΔV = ρ × A Δy.

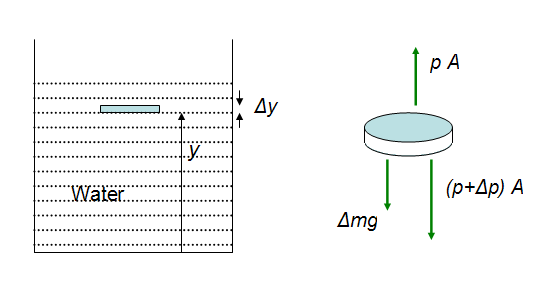Figure 14-1: Pressure in a small body of water inside a container.
Image ©2005 DiscoverHover

Since the fluid has no horizontal or vertical acceleration, the net forces in these directions are zero. The horizontal force comprises the push of the pressure along the circular disk. This is symmetric and cancels out. In the vertical direction the pressure at the top of the element is p, and at the bottom it is p + ΔP. There is a downward gravitational force acting on the body which is equal to Δmg. The vertical forces on the small body are shown in Figure 14-1. Equating the vertical forces to zero, to satisfy the equilibrium condition, we get:

p × A − (p + Δp) × A − ρ × g × A Δy = 0

We can solve this equation for ρ × g to get the relation:

ρ × g = −Δp / Δy

This equation tells us about how pressure varies with the elevation above some reference level in a fluid in static equilibrium. As the elevation increases the pressure decreases because there is less weight pressing down on higher regions. This is indicated by the negative sign.

Robert Boyle
1627 – 1691

A gas confined in a container is an example of a complex system which is difficult to analyze by Newton’s laws of motion. The gas molecules can collide inelastically with one another or with the wall of the container and can exchange energy in a number of different ways. A model which is known as ideal gas model has been developed to simplify this problem. Several appropriate assumptions have been made to solve for different macroscopic properties of gas such as pressure, temperature, etc.

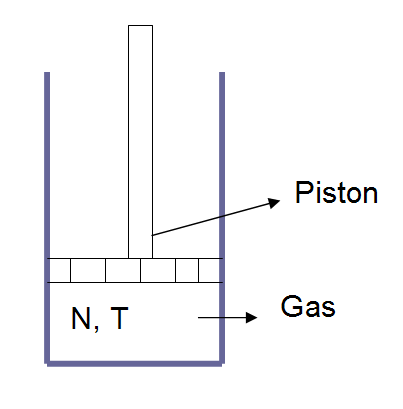
Figure 14-2: An Ideal Gas with a Piston
Image ©2005 DiscoverHover

Assume an ideal gas with a number of particles N and at temperature T. We change the pressure (by changing the weight on the piston) and measure the resulting volume. This results in an inverse relationship between pressure and volume and is known as Boyle’s law.

P = C / V

Here C is the proportionality constant. This is a number based on the number of particles of the gas, N, and the temperature T.

Quiz Questions.

1. An ideal gas at pressure P expands to twice its starting volume, keeping the number of particles N and the temperature T constant. What would be the change in pressure during this process?
2. A tall cylinder is filled with water. Arrange the following in ascending order of their pressures.
   
   1. The bottom of the cylinder.
   2. A height half of that of the cylinder and at the center of the cylinder.
   3. A height half of that of the cylinder but at a point on the side of the cylinder.
   4. The top surface of the water level.