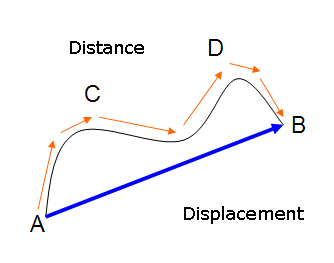
Figure 5-1: Distance and displacement
Image ©2005 DiscoverHover
DiscoverHover CURRICULUM GUIDE #5
KINEMATICS
© 2005 World Hovercraft
Organization
| NAME | DATE |
Kinematics is the study of motion or movement. When an object moves from one place to another, there are many numbers that describe its motion. The basic quantity, on which everything else is based, is the position of the object. This refers to the physical location of the object, so if the position is changing then the object is moving. If the position is not changing, then kinematics is not relevant. The study of objects that are not moving is called statics. The position of an object is usually described either on a coordinate plane or measured in terms of some other point. Many times, this other point is the place where the object is positioned when you start observing it. When the object moves, it has to be moving in a certain direction. The direction in which an object moves is the difference between a scalar and a vector, as we discussed in guide #3.
Distance traveled between two points is the actual distance a particle traverses between two points and is not a measure of direction, while displacement is a measure of both distance and direction. Displacement is the minimum distance connecting the initial and final position of the particle and has a direction from the initial to the final points. Sometimes this is called “as the crow flies” because crows fly in straight directions. In Figure 5-1, the distance is the length of the path ACDB while the displacement is a measure of AB pointing from A to B.

Figure 5-1: Distance and displacement
Image ©2005 DiscoverHover
Imagine your DiscoverHover One hovercraft traveling along a circular path with radius r equal to 150 feet [45.72 m] as shown in Figure 5-2. After one complete revolution (starting from A and returning back to A) your hovercraft traveled a distance equal to 2πr. Hence the distance traveled is 942.9 feet [287.4 m] because the value of 22 divided by 7 can be used to represent π.
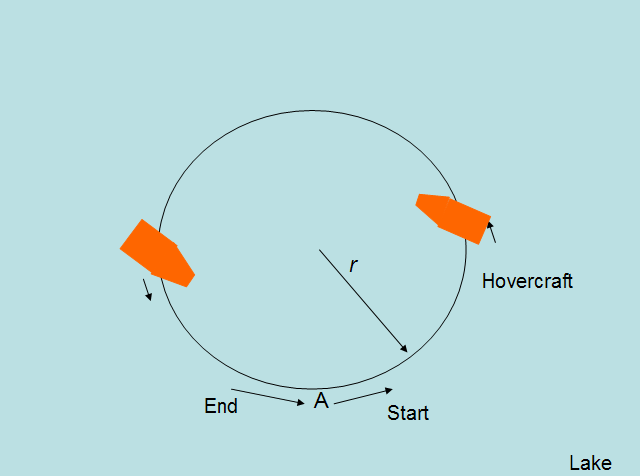
Figure 5-2: Hovercraft traveling in a circle
Image ©2005 DiscoverHover
Since the minimum distance between the starting point and the final point is zero, the displacement of the hovercraft is zero feet [0 m]. The unit of distance is feet or meters; the unit of displacement is feet or meters with direction from the initial to the final point.
Speed is a change in an object’s position with respect to time. This can be found by measuring how far an object travels in a certain amount of time. For example, if a hovercraft traveling at a constant speed (a speed that is not changing) goes 100 miles [161 km] in two hours, its speed was 50 mph [80.5 km/h]. Just divide how far the hovercraft traveled by how long it took to get there. Often the term velocity is used instead of speed, but these two terms are different. Velocity is a measure of both speed and direction of motion. Imagine one hovercraft, traveling 60 mph [96.6 km/h] north on a river, and another hovercraft, traveling 60 mph [96.6 km/h] south on a river. These two hovercraft would have the same speed, but they would have different velocities because they are traveling in different directions. As you can see, velocity is a more detailed description of how fast something is traveling. An equation for calculating velocity is given below.
Velocity = change in position / change in time
Acceleration measures the change in velocity with respect to time. As the term is commonly used, it means an increase in speed. However, it can also mean a decrease in speed. Since velocity is a vector and acceleration is a change in velocity, an acceleration does not have to have any change in speed at all. If a moving object is turning, then the direction, and therefore the velocity, is changing. This means that a change in direction is an acceleration even when the speed does not change.
In our world, objects are constantly accelerating and decelerating, and this can become quite difficult to test with a mathematical model. If we look only at cases in which the acceleration is constant, it becomes much easier to model and to calculate. In fact, we can model any motion along a straight line using only 4 formulas as long as we assume acceleration is always constant.
| Formulas for Motion when Acceleration isn’t Changing |
|
x = x0 + 1/2 × (v + v0) × t .... 1 x = x0 + v0 × t + 1/2 × t2 ...... 2 v = v0 + a × t ........................ 3 v2 = v02 + 2 × a × (x - x0) ..... 4 |
Table 5-1: Formulas for motion when acceleration is constant
In these formulas, x refers to the position of the object, v refers to its velocity, a gives its acceleration, and t gives the time at which these variables are measured. You can see that some of the variables have subscript zeros next to them. For example, x0 is pronounced “x naught” (sounds like “not”). These are used to represent initial conditions, so x0 represents the position of the object initially (at time t = 0), while x represents the position of the object at time t. We’ll do a few examples to see how these formulas work.
|
Example 1: Solution:
Now we need to find one of the formulas just mentioned that has the one variable we’re looking for as well as variables for which we have values. It looks like formula 4 has everything we need and nothing we don’t. Now we can put in all the values and calculate the final velocity. v2 =
v02 + 2 × a × (x
− x0) .... 4 500 ft [152 m] from where it started, the hovercraft will be traveling 70.7 ft/s [21.50 m/s]. |
|
Example 2: Solution:
If we start by just trying to find x, it looks like equation 2 is the one to use. x = x0 +
v0t + 1/2 × a ×
t2 .... 2 We know that the hovercraft will be 250 ft [76.2 m] away after 10 s, now we need to find how fast it will be going when it gets there. We can find this with equation 3. v = v0 + a
× t .... 3 After 10 s, this hovercraft will be 250 ft [76.2 m] away from where it started, traveling 50 ft/s [15.2 m/s]. |
|
Example 3: Solution:
For this one we’re going to use equation 1, but v is buried inside the equation so we have to get it out. x = x0 + 1/2 ×
(v + v0) × t .... 1 Our calculation shows that the speed of the hovercraft increases from 50 ft/s [15.24 m/s] to 70 ft/s [21.37 m/s] by the time it reaches the tree. |
As you can see in the examples, the trick to figuring out which formula to use for these problems is to list all the variables for which you have values and the variables you want to find. Choose a formula that has only one unknown variable and calculate it.
Quiz Questions!
| ©2005 World Hovercraft Organization All rights reserved. Copies of this Curriculum Guide may be printed for classroom use exclusively by DiscoverHover registered members. This Curriculum Guide and all materials contained in the DiscoverHover web site are protected by copyright laws and may not be reproduced, republished, distributed, or displayed on any other web site without the express prior written permission of the World Hovercraft Organization. |